Day 9 – Segments of Tangents
and Secants
In
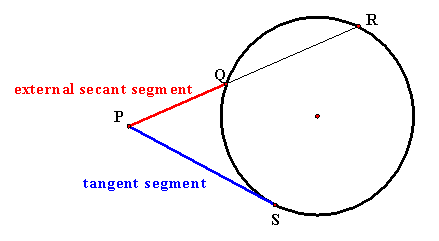
the figure, 
is called a tangent
secant because it is tangent to the circle at an endpoint. Similarily, 
is a secant segment
and 
is the external
segment of . The external
segments are those that lie outside the circle.
There is a special relationship between secant
segments and external secant segments stated in the following theorem:
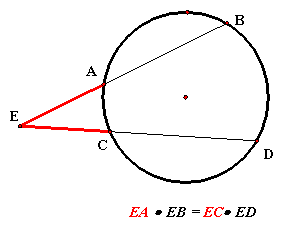
If two secant segments share the
same endpoint outside a circle,
then the product of the length of
one secant segment and the length of its external segment equals the product of
the length of the other secant segment and the length of its external
segment.
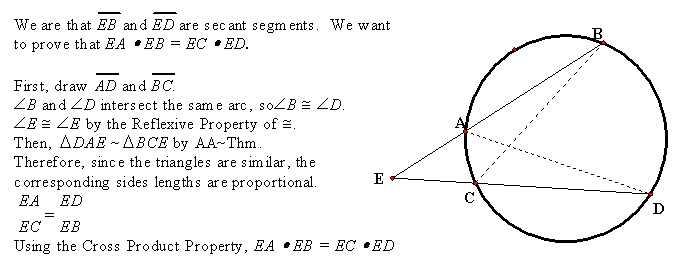
Proof:
In the next theorem, we observe a relationship between
a secant segment and tangent segment.
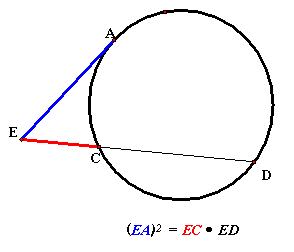
If a secant segment and a tangent
segment share an endpoint outside a circle, then the product of the length of
the secant segment and the length of its
external segment equals the square
of the length of the tangent segment.
Proof:
